今回は、「コラッツ予想物語」(1万字)です。
前回の「コラッツ予想」をどのように考えて、この結論に至ったのかを物語にしました。
いろいろな問題を解く参考になったら、ありがたいです。
興味のある方は、「コラッツ予想物語」をみてください。

第13回日経「星新一賞」に応募しましたが、残念な結果となりました。
「数学とあそぼう」というテーマで、ブログを始めました。
今回は、「コラッツ予想」です。
コラッツ予想とは、「すべての自然数は、偶数なら2で割り、奇数なら3倍して1をたす、を繰り返すと必ず1になるはずだ」というものです。なぜ、必ず1になるのでしょう。考えてみました。
結論は、
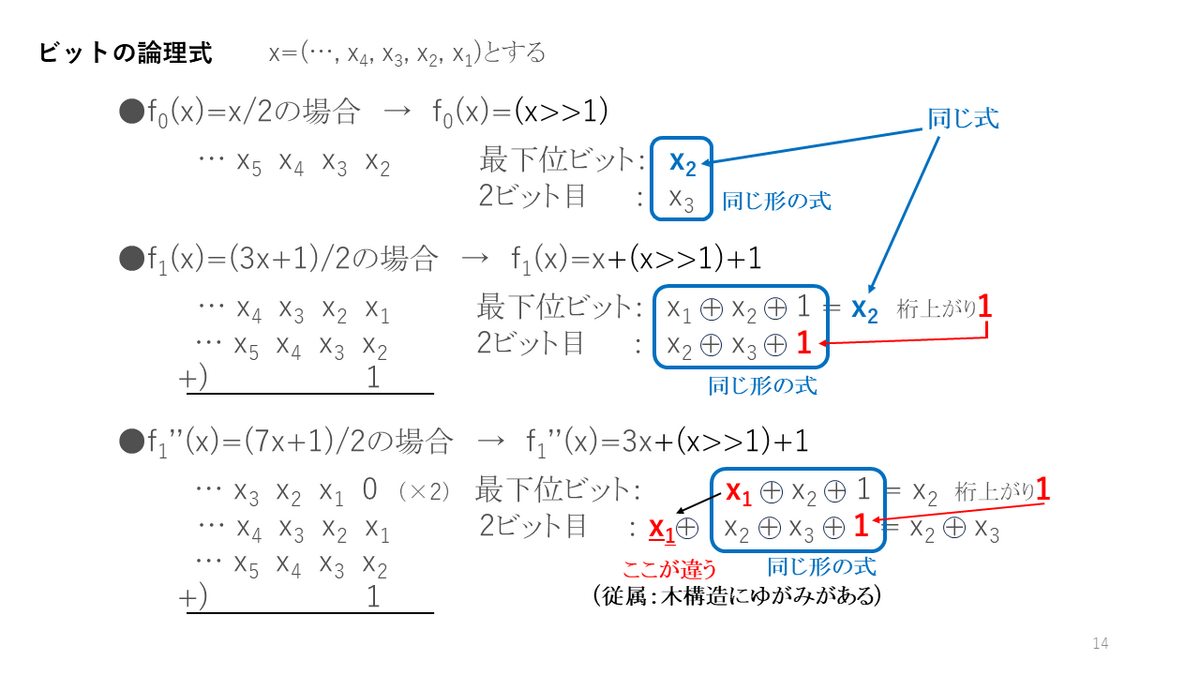
1. コラッツ予想を論理式で表すと、とてもきれいで、バランスのとれた式になっている。
例えば、「奇数なら3倍して」を、「5倍」、「7倍」に変更すると、バランスの悪い式になってしまい、必ず1にはなりません。
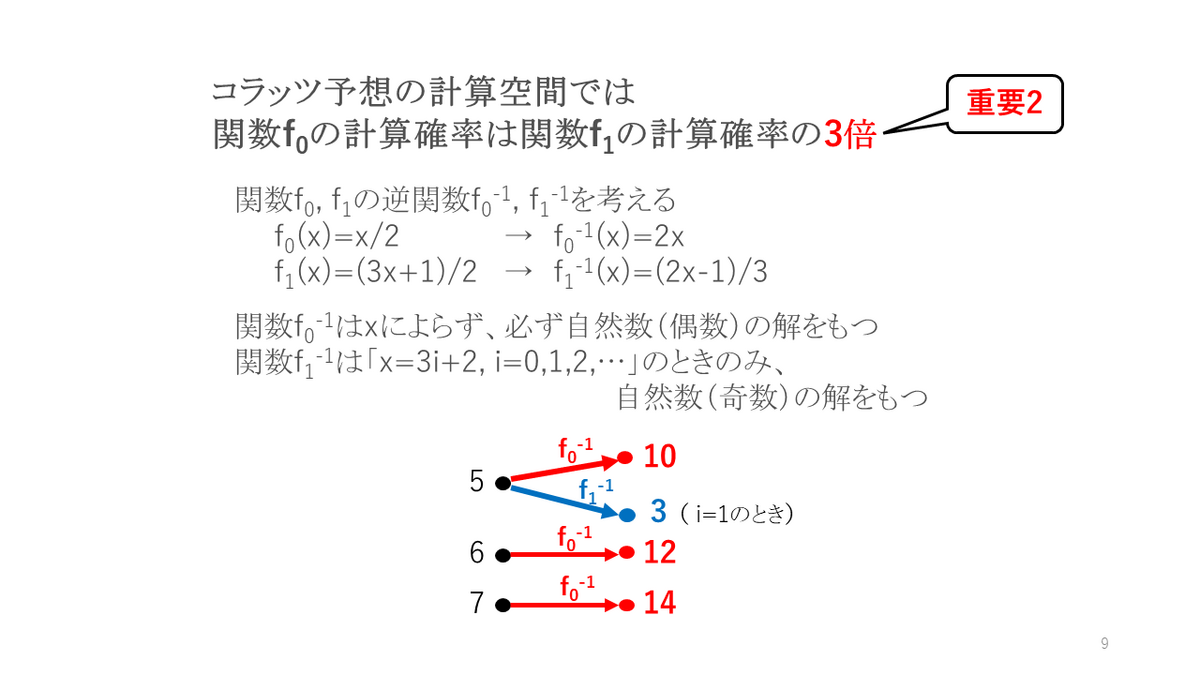
2. コラッツ予想の計算空間は、小さくなる圧力が大きくなる圧力の3倍である。
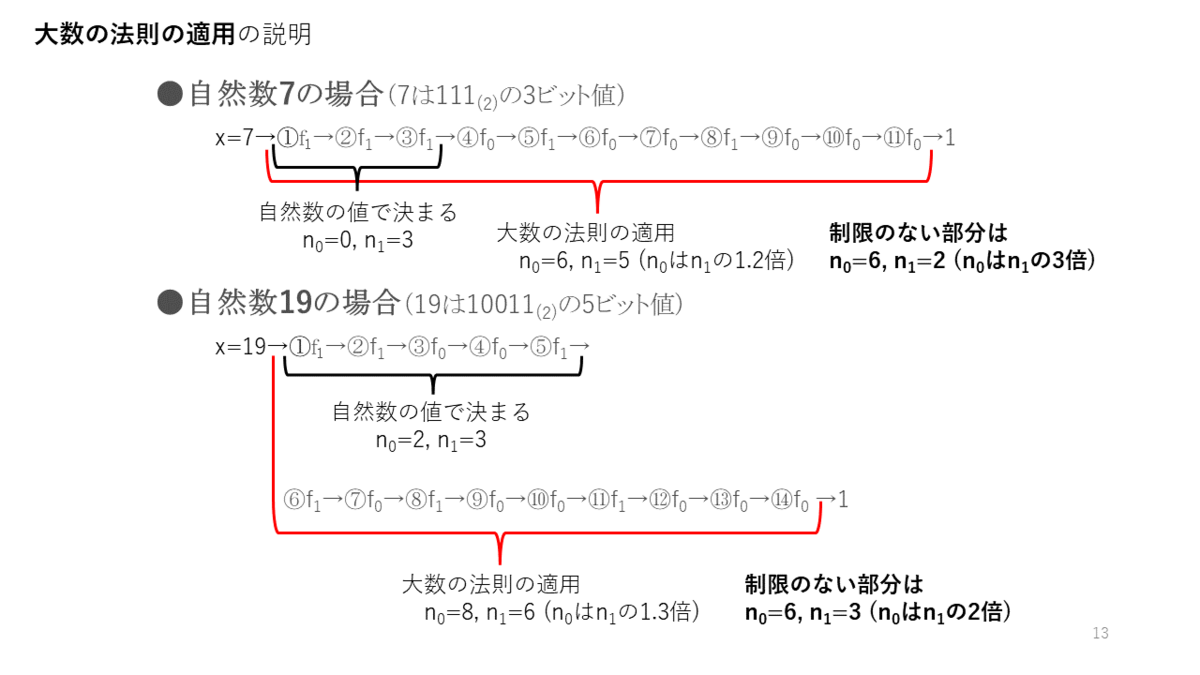
以上のことから、計算を繰り返すと、必ず1になるのです。
詳細は、「コラッツ予想 なぜ1になるのか」です。
より詳細な説明を知りたい方は、「辻󠄀原整数論セミナー」、「Jxivへの投稿論文」をみてください。
論文の補足説明をします。
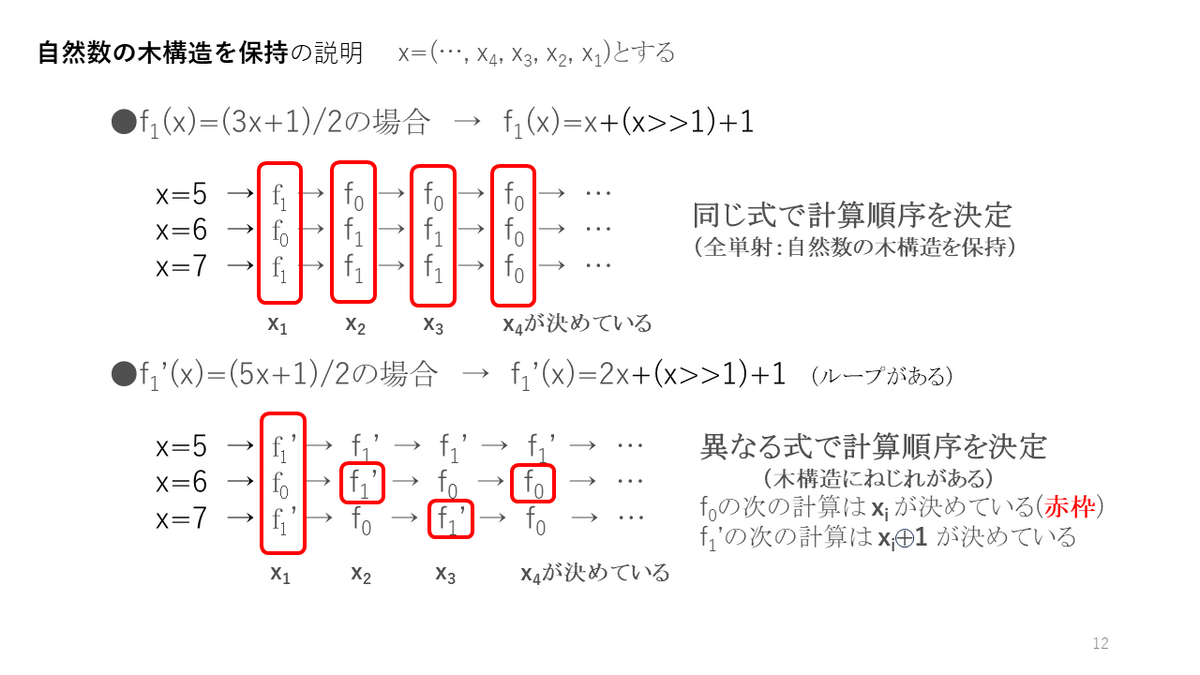
自然数の木構造を保持している場合は、”1, 2, 3, 4, …”と1ずつ順に数が大きくなることを意味しています。これが、3倍のときです。
5倍のときは、親が1の場合、その子の左右が入れ替わるので、3ビット値で考えると、”7, 6, 5, 4, 3, 2, 1”の順になります(ただし、親とその親のどちらも1の場合は入れ替わらない)。これを、ねじれた状態と呼んでいます。
7倍のときは、親とその親のどちらも1の場合、その親の子の左右が入れ替わるので、3ビット値で考えると、”1, 2, 7, 4, 5, 6, 3”の順になります。これを、ゆがんだ状態と呼んでいます。
従って、コラッツ予想は「3倍」でなければならないのです。
※Jxivとは、国立研究開発法人科学技術振興機構(JST)が運営しているプレプリントサーバ(Jxiv, JSTプレプリントサーバ)です。残念ながら、却下されてしまいました。